ライプニッツ

哲学者、博物学者ライプニッツはホイヘンスに数学の手ほどきを受けた。デカルトの孫弟子に当たる
ヘンデル(1685-1759)とライプニッツ(1646-1716)は同じ君主に仕えた。
イギリス王室に仕えていたヘンデルは、かって袖にしたハノーバー選帝侯がハノーバー/ウィンザー朝の始祖ジョージ1世として海を渡って来たので(1714)、大慌てで水上の音楽などを作って、興をかった。
ライプニッツはニュートンとの微分の先取論争の渦中にあり、ハノーファーに置き去るりにされた。今ではハノーバーにライプニッツ大学がある。

行列式

関孝和

ベルヌイ一族

多くの数学者や科学者を輩出した。
ベルヌイ一家は音楽のシュトラウス一家と並んで仲の悪いことでも有名。
今日のライプニッツ流微分、積分の普及はヤコブと弟のヨハンの貢献が大きく、弟子のオイラーに受け継がれた。

ベルヌイ試行

兄のヨハンに帰する。結果がYes/Noすなわち0/1で決まるトライアルをベルヌイ試行と言い、 2項分布の基礎となる。サイコロを振って1の目が出るか否かはベルヌイ試行であり、どの目が出るかはベルヌイ試行と異なる。

ベルヌイ数

関孝和

ベルヌイの懸垂曲線

ヨハン・ベルヌイがニュートンを困らせようと懸賞問題を出して返り討ちにあった問題。カテナリー曲線に帰着する。 \[ y= a cosh(\dfrac{x}{a})=\dfrac{a(e^{\dfrac{x}{a}}+e^{-\dfrac{x}{a}})}{2}\]

require 'plot numeric trig'
 plot a;  +/ ^ 1 _1 */ a=. steps _1 1 100

 plot a; cosh a=. steps _1 1 100

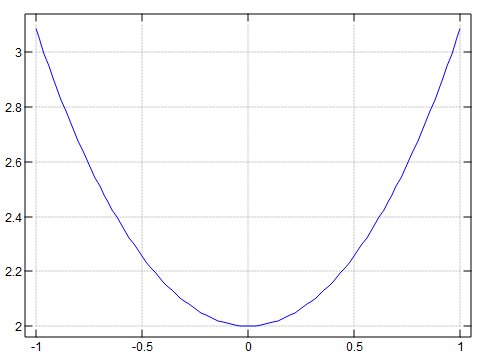yを反転させるとセントルイスのゲートウエイアーチになる。

 plot a; - +/ ^ 1 _1 */ a=. steps _1 1 100

オイラー（1707－1783）

スイスのバーゼル生まれ。ベルヌイに見いだされた。
2度にわたってロシアのエカテリーナ（1，II世）に仕え、政争に巻き込まれないように常に忙しく研究を続け、ペテルブルグで平穏に終焉を迎えた。
途中の25年（1741－1766）はベルリンのアカデミーでヴィルヘルム2世に使えた。
オイラーの亡くなった年にパリでモンゴルフィエ兄弟が初の気球飛行を成し遂げた。

美しい公式

\[ e^{i \pi}+1=0 \]

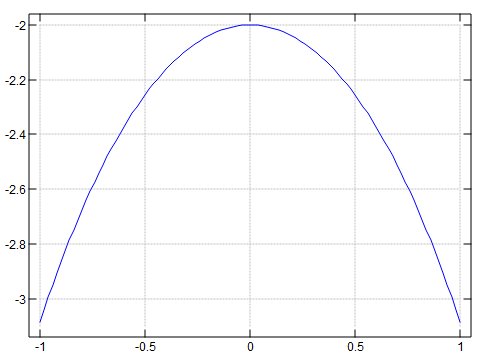
require 'numeric'

   clean  ^  0j1* 1p1
_1

\(\pi , 2 \pi , 3 \pi , 4 \pi \cdots \)とすると

  1p1* 0j1* >:i.6
0j3.14159 0j6.28319 0j9.42478 0j12.5664 0j15.708 0j18.8496
   clean 1x1 ^ 1p1* 0j1* >:i.6
_1 1 _1 1 _1 1

\[ e ^{i \theta}=cos \theta + isin \theta\] +. で実部と虚部を分離してある

\( e^{i \theta} \)

\( cos \theta + i sin \theta \)

   +. ^  0j1*  >:i.10
 0.540302  0.841471
_0.416147  0.909297
_0.989992   0.14112
_0.653644 _0.756802
 0.283662 _0.958924
  0.96017 _0.279415
 0.753902  0.656987
  _0.1455  0.989358
 _0.91113  0.412118
_0.839072 _0.544021


 +. +/ 1 0j1 * >(cos ;sin)>:i.10
 
 0.540302  0.841471
_0.416147  0.909297
_0.989992   0.14112
_0.653644 _0.756802
 0.283662 _0.958924
  0.96017 _0.279415
 0.753902  0.656987
  _0.1455  0.989358
 _0.91113  0.412118
_0.839072 _0.544021