　　　　　　　　　　　　　　　　　　　　　　　　　　　　Ｊ研究会資料(1999

　　　　　　　　　　　　　　　　　　ＪAPLAシンポジュウム資料(2004.12.11）

　　　　　　　ノンパラメトリック統計学とＪ言語

　　　　　　　　　　　　　　　　　　　　　　　帝京平成大学　鈴木義一郎

　　　§１適合度検定

　一般に、連続な分布関数Ｆ(ｘ)に従う確率変数に対して、大きさの順番に並べ直した{ }を「順序統計量」という。さらに

で定義されるものを「経験分布関数」といい、

Fn(x) → F(x) n → ∞ for all x

という性質がある。そこで

といった統計量が定義できる。これらはコルモゴルフの「Ｄ－統計量」と呼ばれているもので、特には「片側統計量」である。またこれらの統計量の分布は、Ｆ(ｘ)という分布形に依存しないで定まることから「分布に依らない(distribution-free）統計量」とも呼ばれている。

　一般に、,ｉ＝１,２,……… ,ｎのように変換すると、ＸがＦ(ｘ)に従うときには，これらは[０,１]上の一様分布からの順序統計量になる。そこで、当該データから、の経験分布関数([０,１]上の関数になる！)を描いてみて、これが対角線上から極端に離れる(つまりやの値が大きくなる)ようならば、一様分布からの順序統計量ではない、したがって「観測データがＦ(ｘ)には従わない」と判断できる。特にＦとして正規分布関数を考えれば、正規分布か否かを識別することができるというになる。

　ところが問題は、この種の統計量が適合度を測っているのでなく、“非適合度”を測っているに過ぎないという点である。つまりデータ数が少ないと、どんな分布を仮定しても、情報不足の故に、その分布に従わないという結論が得られない、つまりその分布に従うことを容認せざるを得ないことになる。結局、どんな分布を仮定しても否定されないということは、「どんな分布を仮定すれば良いか？」という問の回答が得られないということになる。逆に、データ数が非常に多い場合には、どんな分布を仮定しても「その分布には従わない」という結論になるケースが多くなる。結局、どんな分布を仮定しても否定されるということで、やはり「どの分布を仮定すれば良いか？」に対する回答は得られない。要するに、データが少なすぎても多すぎても分布を特定できないということから、「適合度検定は使いものにならない」ケースが圧倒的に多いというのが結論である。

　それはともかくも、片側統計量の確率分布の求め方の概略を紹介してみよう。まず

という値を算出する。そこで

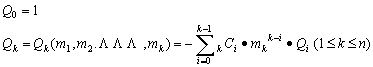
という多項式群を定義して

という関数を求めると

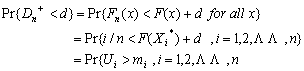
が求める確率分布を与えることになる。

　次のデータは、昭和３５年の栃・若時代の幕内力士４３人の体重を、大小の順に並べたものである。

85 88 95 97 101 101 102 103 103 104 105 105 105 107 109

109 110 110 111 111 111 112 112 114 115 115 116 116 116 120

120 120 122 124 128 128 131 135 141 146 148 150 150

このデータを「WAT」という変数に入力して、これを「stand」という関数によって基準化すると

0.3": 4 10 $ stand WAT

_1.604 _1.478 _1.257 _1.132 _0.943 _0.659 _0.659 _0.565 _0.502 _0.502

_0.471 _0.471 _0.439 _0.408 _0.408 _0.376 _0.345 _0.282 _0.219 _0.502

_0.156 _0.156 _0.156 _0.124 _0.093 _0.093 0.093 0.285 0.348 0.348

0.379 0.379 0.474 0.474 0.505 1.229 1.481 1.607 1.922 4.125

0.153 1.179 _0.728 0.298 _0.738 _0.718 _0.515 2.399 _0.709 _0.621

この値に標準正規分布関数Φ(・)をかぶせてみると

0.3": 4 10 $ E=:ndf"0 /:～ stand WAT

0.054 0.070 0.104 0.129 0.173 0.255 0.255 0.286 0.308 0.308

0.319 0.319 0.330 0.342 0.342 0.353 0.365 0.389 0.413 0.438

0.438 0.438 0.438 0.451 0.463 0.463 0.538 0.612 0.636 0.636

0.648 0.648 0.682 0.682 0.693 0.890 0.931 0.946 0.973 1.000

といった結果が得られる。

一方、一様分布の理論値のほうは

i/n,(t=i/n) ,i=1,2,…………,n

であるが、両側統計量の場合の近似に用いるためには

(i-0.5)/n,(t=i/n) ,i=1,2,…………,n

を考えたほうがよい。

4 10 $ T=:((i.+0.5"_)%])40

0.0125 0.0375 0.0625 0.0875 0.1125 0.1375 0.1625 0.1875 0.2125 0.2375

0.2625 0.2875 0.3125 0.3375 0.3625 0.3875 0.4125 0.4375 0.4625 0.4875

0.5125 0.5375 0.5625 0.5875 0.6125 0.6375 0.6625 0.6875 0.7125 0.7375

0.7625 0.7875 0.8125 0.8375 0.8625 0.8875 0.9125 0.9375 0.9625 0.9875

　そこで、{Ｅ－Ｔ}の絶対値をとると

4 10 $ D=:|E-T

0.042 0.032 0.042 0.041 0.060 0.117 0.092 0.099 0.095 0.070

0.056 0.031 0.018 0.004 0.021 0.034 0.047 0.048 0.049 0.049

0.074 0.099 0.124 0.137 0.149 0.174 0.124 0.075 0.076 0.101

0.115 0.140 0.130 0.155 0.169 0.003 0.018 0.008 0.010 0.012

のような結果になる。これらの値の最大値は

>./D

0.174489

である。また、「stat_d」という関数を適用すれば

stat_d stand WAT

0.174489

のように同じ結果が得られる。

ところで片側統計量の５％点や２.５％点は、「percent_5」や「percent_2_5」という関数を用いて

percent_5 40

0.210115

percent_2_5 40

0.18913

のように求められる。片側統計量の２.５％点がほぼ両側統計量の５％点になるので、Ｄnの値が０.２１より大きければ正規分布の仮定が棄却できる。観測結果は 0.1745であるから、有意水準５％では棄却できない。つまり正規分布でないとは結論できない。また最近の幕内力士の体重データも「WTW」という変数に入力して、

stat_d stand WTW

0.140572

といった結果で、｢WAT」の場合より偏差が小さく、より正規分布に近いことが分かる。

　さらに、一様分布からのデータについても試してみると

stat_d stand ([:?]$10000"_) 40

0.0959442

stat_d stand ([:?]$10000"_) 40

0.103789

といった例が示すように、正規分布であるとの仮説棄却されない。つまりデータ数が４０個程度では、一様分布や２重指数分布などからの乱数を使って実験してみても、正規分布であるとの仮説はほとんど否定できない！

【Ｊによるプログラム】

mvalue=:0:>.(-@{:*%@{.)+(>:@i.%])@{. NB. m(i)=m(i;n,d)(1≦i≦n)

weight=:(i.!])@[*(<:@[{mvalue@])^[:|.1:+i.@[

NB. W(k,i)=B(k,i)m(k)^(k-i),(0≦i≦k-1)

qvalue=:>@{.;>@{:,[:-[:+/#@>@{:weight>@{.

NB. Q(k)=Q(n,k)=-{Q(0)W(k,0)+Q(1)W(k,1)+ +Q(k-1)W(k,k-1)

function=:4 :'+/((1.x.+1)!x.)*,>}.qvalue^:x.(x.,y.);1'

NB. P(n,c)=B(n,0)Q(n,0)+B(n,1)Q(n,1)+ +B(n,n)Q(n,n)

derivative=:4 :'(x."_function])D.1 y.'

ratio_5=:(function-0.95"_)%derivative

percent_5=:([:([:{:({.,{:-{.ratio_5{:)^:_)],1:)%]

ratio_2_5=:(function-0.975"_)%derivative

percent_2_5=:([:([:{:({.,{:-{.ratio_2_5{:)^:_)],1:)%]

nden=:[:%&(%:o.2)[:^*:%_2: NB. standard normal density]

grid=:*&((>i.499)%500)

ndf=:0.5"_+%&500*([:mean[:nden 0:,])+[:+/[:nden grid

NB. standard normal distribution function

stat_d=:[:>./[:|([:ndf"0/:～)-[:((i.+0.5"_)%])# NB. D-stat.

　　　§２順位和検定(Mann-Whitney test)

　§１では、データ数が少なすぎても多すぎても分布が特定できないことを指摘したが、データが多ければ、ある種の条件を満たす限り『中心極限定理』が成り立つことから、正規分布を仮定して議論を行なうことができる。問題は、データ数が少なすぎる場合である。正規分布であると確信できれば、ｔ－推定やｔ－検定を用いることができるが、どんな分布に従うのか判然としない場合、強引に正規性を仮定して議論するのは危険である。そこで、分布形を規定しなくても利用できる、いわゆる「ノンパラメトリック法」を用いて検定などを行なえばよいということになる。

　例えば

X=:9.3 19.9 0.2 10.8 0.1 0.3 2.4 32.5 0.4 1.3

Y=:8.4 23.5 113 97.3 53.2 28.7 7.6 44.7 85.2 49.1 105.1 30.3

といった２組のデータが与えられていて、平均の差異について検定したいとする。

　まず平均は

(MX=:mean X),(MY=:mean=:+/%#)Y

7.72 53.8417

であるから、明らかに差がありそうである。

　さらに分散も

(VX0=:var X),(VY0=:var=:[:mean[:*:]-mean)Y

106.716 1284.64

と算出されるから、等分散も仮定できない。

　そこでまず、正規分布を仮定できるものとして議論してみよう。まず最初に、不偏分散を求めると

(VX=:var_u X),VY=:(var_u=:[:(+/%<:@#)[:*:]-mean)Y

118.573 1401.43

である。さらに

ww=[VX/m+VY/n]2/{VX2/m2(m-1)+VY2/n2(n-1)}

という値を超える最小の整数をｗとするとき、

という統計量が、等平均の仮定の下では自由度ｗのｔ－分布で近似できることを利用して検定できる。これは「ウェルチの検定」と呼ばれているものである。ｗｗや統計量ｔの値を求める関数は次のように与えられる。

welch0=:[:(*:@{.%{:)[:+/"1[:>(](],*:@]%<:@#@[)var_u%#)L:0

welch=:[:(-/@{.%[:%:+/@{:)[:|:[:>(mean,var_u%#)L:0

この例では、

(welch0 X;Y),welch X;Y

0.556572 _4.06642

である。ｔの絶対値４.０６６は、自由度(ｗ＝１)のｔ－分布の片側５％点６.３１４より小さいから、等平均の仮説は棄却できない。平均がかなり異なっている感じなのに等平均の仮説を棄却できないということは、正規分布の仮定がオカシイということになる。

　そこで、分布形によらない「ノンパラメトリック検定」を試してみよう。平均の差異を検出する最も典型的なものが、「順位和検定」とか「Mann-Whitney検定」と呼ばれている方法である。

　一般に、同じ連続分布から

のような２組のデータが与えられているとする。全体を一緒にして並べ直したときの、Ｘのほうの順位を（）として

という「順位和」を考える。そこで、次のような関数を考える。

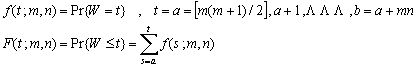
定義から、次のような漸化関係の成り立つことが分かる。

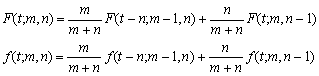
したがって、ｍやｎの値がそれほど大きくない場合には、正確な％点の値を直接求めることができる。

　さらに、Ｗの期待値と分散は

E{W} = m(m+n+1)/2 = M　，V{W} = mn(m+n+1)/12 = nM/6

で与えられる。また４次のキュミュラントも

K = -mn(m+n+1)×{(m+n)(m+n+1)-mn}/120 = -nM{M+nM/m-mn/4}/30

のように与えられるから、

と置いて

F(t;m,n) = Φ(V)

という関係によって近似することができる(Φは標準正規分布関数)。

　さて、「rank」という関数は２組のデータ全体に順位を与えるものである。

rank X,Y

9 11 2 10 1 3 6 15 4 5 8 12 22 20 18 13 7 16 19 17 21 14

+/ 10{. rank X,Y

X ranksum Y

つまり「ranksum」は、Ｘの順位の合計Ｗである。なお、ＷにＹのほうの順位和１８３を合計すると２５３になり、これは(m＋n)(m＋n＋1)/2のように、標本数によって定まる量である。つまり、ＸかＹのどちらか一方の順位和だけに着目すればよい。さらに、ｍ＝10，ｎ＝12のときの５％点(の近似値)を求める関数「rminimax」を用いて

rminimax 10,12

89 141

という値が算出できる。この近似式は驚くほど精度がよい(ｍ≦ｎ≦１２という範囲では、(３,９)と(５,１０)のときだけ１だけ安全なほうに異なっている)。

　さて与えられた順位和の66は、下方の限界値89より小さく、メデタク、平均に差のあることが検出できた。また、力士の体重のデータにも適用してみると

WTW ranksum WAT

1133

が順位和である。この場合の５％点が

rminimax 40,43

1498 1862

であるから、平均差は高度に顕著であることが分かる。さらに

W1=:88 103 110 110 112 124 128 141 148

W2=:113 132 137 138 139 142 144 148 165 204

は、それぞれ WTW,WATというデータから10個ずつランダムに抜き出したものである。このような小さめのデータにも適用してみると

W1 ranksum W2

が順位和である。この場合の５％点は

rminimax 10,10

82 128

であるから、やはり平均に差のあることが検出できる。

【Ｊによるプログラム】

NB. TEST STATISTIC

rank=:1:+(i.@#=//:)+/ .*i.@#

ranksum=:[:+/#@[{.[:rank, NB. rank-sum test statistic(dyadic)

NB. Exact Probability

add=:(([:<"1[:(],.[:}.i.)1:+#),.]);(<<1 0)"_

left=:>@{.@{.>@{.

right=:{:@{.@{.,{:@>@{:

middle=:([:+/[*(({:@[$0:),>@{.@]),>@{:@])%+/@[

next=:}.@>@{.;[:<>@{:,[:<left middle right

first=:3 :'}.>{:next^:(#y.)add y.'

second=:([$0:)(,+,～)-:@]

prob_list=:[:(],[:<>:@#@]second[:([:>{:)first

start=:[:<:[:([:+/>:@i."_1>:@i.

minpt=.start@#+([:+/0.05"_>:+/＼)&>

total=:(1:+i."0)([*>:@+)]

minmax=:[:(],.total@#-])minpt

percent=:}."1,([:(minmax;<@,.@])prob_list>@{:"1

NB. Approximation

rm=:[:-:<./**1:++/

ru=:%:@(12"_%*/*1:++/)@]*[-0.5"_+rm@]

rv=:ru*1:+(*:@ru-3:)*(((]*>:)@+/-*/)%40"_*}:*rm)@]

range=:-:@(]*>:)@{.+[:i.*/ NB. a=m(m+1)/n,a+1,---,b=a+mn

rmin=:_1:+[:{:(_1.65"_>:[:,range rv"0 1])#range

rminimax=:(*/+(]*>:)@<./)(],.-)rmin NB. lower & upper 5%-points

　　　§３置換検定(Pittman test)

　§２では、平均の差異を検出する最も典型的なノンパラメトリック検定として、「順位和検定」を考えた。もし与えられたデータが「順序尺度」であれば、順位だけを利用する方法を考えるのが自然である。しかしデータが「間隔尺度」の場合には、順位だけでなく数値まで利用する考えのほうが合理的である。そこで、ピットマンが提案した「置換検定」という方法を紹介してみよう。

　一般に、同じ平均をもつ母集団から

のような２組のデータが与えられているとする。全体を一緒にして並べ直したものを

とする。(ｍ＋ｎ)個からｍ個を取り出す組合せの数はＮ＝あり、各組合せのｍ個の和を小さいほうから順番に並べたものを

(*)

とする。最小値と最大値は、明らかに

である。そこで、Ｘのほうのデータの和が(＊)のどの辺に位置するかに注目する。もし平均に差がないとすれば、真中辺に位置するし、Ｘの平均がＹの平均より小さい(大きい)場合には、左端(右端)のほうに位置することが期待される。結局、Ｘのほうの和が左右いずれかの極端に偏っているときに、等平均の仮説が棄却できることになる。ただこの方法は、ｍやｎがほどほどに小さくないと、組合せの数が大きくなって計算量が膨大になるという欠陥もある。例えば、ｍ＝１０ｎ＝１２としてみると、Ｎ＝646646である。

　まず

A=:3 4 ] B=:2 6 7

といった２組のデータで考えてみる。ｍ＝２，ｎ＝３の場合の組合せは

comball 2 3

1 1 0 0 0

1 0 1 0 0

1 0 0 1 0

1 0 0 0 1

0 1 1 0 0

0 1 0 1 0

0 1 0 0 1

0 0 1 1 0

0 0 1 0 1

0 0 0 1 1

のように１０通りある。各組合せに対する２個のほう和は

2 5([:+/"1([:comball#&>@;)#,)3 6 7

7 5 8 9 8 11 12 13 10 9

のように与えられる。

　そこで、これらの値を順番に並べ直したとき、Ａという組合せの和がどの位置にあるかは、「position」という関数を用いて

2 5 position 3 6 7

1 1 0 0 0 0 0 0 0 0

のように小さいほうから２番目にあることが分かる。

2 5 permute 3 6 7

0.2

　次に、ｍ＝６，ｎ＝８の場合の例として

]XX=:4}./:～X

1.3 2.4 9.3 10.8 19.9 32.5

]YY=:_4}./:～Y

7.6 8.4 23.5 28.7 30.3 44.7 49.1 53.2

といった２組のデータについて考えてみる。順位和検定を行なってみると

XX ranksum YY

という結果が得られる。しかし、順位和の５％点は

rminimax 6 8

31 59

であるから、等平均の仮説が棄却されない。ところが置換検定では

+/ XX position YY

となり、ＸＸの和は小さいほうから７８番目のところにあることが分かる。Ｎ＝３００３であるから

78 % 3003

0.025974

また、「permute」という関数を使って

XX permute YY

0.025974

となる。５％の有意水準で、等平均性が棄却できる。

【Ｊによるプログラム】

zero=:[:<(1:,1:+[:{:[:$[:>{.)$0:

body=:[:(((1:,.>@{.),0:,.>@{:)L:1)2:<＼]

more=:]`(],[:-.L:0{:)@.(([:([:(+/<-:@#)@{.@>{:)])

comball=:3 :'>({.y.){(zero,[:more body)^:(_1++/y.)(,.0);,.1'

position=:+/@[>:[:+/"1([:comball#&>@;)#,

permute=:([:+/position)%[:({.!+/)#&>@;

　　　§４連の個数による検定

　§２のデータを大きさの順に並べて

X=:0.1 0.2 0.3 0.4 1.3 2.4 9.3 10.8 19.9 32.5

Y=:7.6 8.4 23.5 28.7 30.3 44.7 49.1 53.2 85.2 97.3 105.1 113

データ全体に順位をつけたとき、Ｘの方の順位は

1 2 3 4 5 6 9 10 11 15

のように与えられ、またＹのほうの順位は

7 8 12 13 14 16 17 18 19 20 21 22

である。これらの順番にしたがって、Ｘのデータには１、Ｙのデータには０をつけると

1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0

といった系列が得られる。このとき、１の連なりや０の連なりのことを「連」といい、各連の大きさを連の「長さ」という。上の例では、長さ６の１の連、長さ２の０の連、長さ３の１の連、長さ３の０の連、長さ１の１の連、長さ７の０の連があり、合計６つの連がある。連の個数をＲ＝Ｒ(ｍ,ｎ）と書くと、１と０が左右に完全に分離した場合は連の個数Ｒが２で、これが最小値である。一般に、ｍやｎの数が大きくなればＲの値も大きくなる。また、２組の標本が同一母集団からのものであれば１や０が入り乱れて連の個数は多くなる傾向を示すが、平均などが違っていれば、１と０が分離しやすくなるから連の個数Ｒは少なくなる。かくて、Ｒの大小によって、２組の標本が同一母集団からのものであるか否かを識別することができる。

　一般に、Ｒの確率分布は

で与えられる。ここで

　この確率の計算はＷの場合より簡単で、かなり大きなｍ，ｎでも正確な値を瞬時に算出できる。この統計量は、ｍ，ｎがかなり大きいときにだけ正規近似を用いるほうがよい。

　Ｒの期待値と分散は

のように与えられる。

　さて、「run」という関数を用いれば

X run Y

1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0

のように０，１の系列が得られ、さらに「number」という関数により

X number Y

といったように、連の個数が求められる。

　次に、「prob」という関数を用いれば、Ｒの正確な確率分布が算出できる。

ｍ＝１０，ｎ＝１２の場合には

0.4": 3 7 $ prob 10 12

0.0000 0.0000 0.0003 0.0014 0.0061 0.0163 0.0429

0.0750 0.1286 0.1543 0.1800 0.1500 0.1200 0.0686

0.0367 0.0138 0.0046 0.0010 0.0002 0.0000 0.0000

である。さらに

0.05(lower,upper)10 12

7 17

が、下側と上側の５％点を与えている。上の例ではＲ＝６であったから、下側５％点より小さく、等平均の仮説を有意水準５％で棄却できる。この結論は、順位和検定の場合と同じである。

　また力士の体重のデータにも適用してみると

WTW number WAT

が連の個数である。またこの場合の５％点は

0.05(lower,upper)40 43

34 51

と与えられ、連の数は極端に少ないことから、やはり平均体重の間にはかなりの差のあることが識別できる。さらに小さなW1，W2といったデータにも適用してみると

W1 number W2

が連の個数である。またこの場合の５％点は

0.05(lower,upper)10 10

6 16

であるから、平均が等しいとの仮説は棄却できない。順位和検定では棄却できたから、連の数による検定は、やや感度が鈍い趣のあることが分かる。

【Ｊによるプログラム】

run=:(1:+i.@#@,)e.#@[{.[:rank,

number=:[:(1:+[:+/[: }.-}:)run NB. number of run test

even=:2:*[:*/! NB. 2*C(m,k)*C(n;k) x=k,y=m,n

odd=:([:*/@["0])+[:*/[!"0] NB. C(m,k)*C(n;k-1)+C(m,k-1)*C(n;k)

comb=:(<:@-:@[even<:@])`(([:(<:,])<.@-:)@[odd<:@])@.(2: [)

prob=:((1:+[:}.i.@+/)comb"0 1])%<./!+/

lower=:1:+[:[:+/[>:[:+/＼prob@]

upper=:2:+[:[:+/[<:[:+/＼[: .prob@]

X run Y

1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0

X number Y

0 even 3 2 ┃ 1 2 3 even"0 1(3 2)

2 ┃12 6 0

([:(,.|.)],<:)2 ┃ 2

2 1

1 2

2(([:(,.|.)],<:)@[);])3 2 ┃ 2(([:(,.|.)],<:)@[)!"1])3 2

┌-─┬-─┐ ┃3 1

│2 1│3 2│ ┃3 2

│1 2│ │

└─-┴-─┘

2 odd 3 2 ┃ 1 2 3 odd"0 1(3 2)

9 ┃5 9 1

(2+i.6)comb"0 1(4 3)

2 5 12 9 6 1

prob 4 3

0.05714429 0.142857 0.342857 0.357143 0.171429 0.0285714

+/ prob 4 3 ┃ 0.05 lower 4 3

1 ┃1

($,+/) prob 10 12 ┃ (lower,upper)prob 10 12

21 1 ┃7 17

　　　§５Ｍｏｓｅｓの検定

　一般に

のような２組のデータが与えられているとき、全体を大きさの順番に並べたものを

と置いて、Ｘ(Ｙ)のデータには１(０)を付ける。そこで、ｈを適当な自然数として、左から(ｈ＋１)番目の１の順位を、右から(h＋1)番目の１の順位をとして

という統計量を考え

となるような限界値を求めて、観測結果がこの値より小さいときに、散布度が等しいとする帰無仮説を有意水準αで棄却できる。ｈの定め方には任意性があるが、ｈ＝[m/4]を考えるのが妥当なところだろう。そこで、特にｈ＝[m/4]としたをＭ(ｍ,ｎ)と表すことにする。

　Moses([２])は、ｋ＝m－2hと置いて、次の関係を示した。

【Ｊ言語によるプログラム】

position=:([:/:～;)e.>@{.

stat_m=:3 :'-/+/(+/＼position y.)<:/(#>{.y)(-,])<.y.%4'

pair=:[:(,: .)[:i.>:

start=:](<:@],-)[:<:[:<.[:-:[

numerator=:[:*/"[:!/"1[: :start(],:+)pair@[

prob_m=:[:(]%+/){.numerator{:

prob5=:[:((1:+[:+/0.05"_>:]){.])[:+/＼prob_m

index=:[:+/"1[>:/[:prob5]

range0=:0:,([:i.>:)+2:*[:<.]%4:

percent_m=:index{[:range0[:{.]

X=.6 8 9 10 11 12 13 14 15 16 20 24

Y=.2 3 4 5 7 21 22 23 25 26 30 32

position X;Y

0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 0 0

3 stat_m X;Y

pair 8 ┃ 8([: :start@](],:+)pair@[)10

0 1 2 3 4 5 6 7 8 ┃ 1 6435

8 7 6 5 4 3 2 1 0 ┃ 3 3432

8 start 10 ┃ 6 1716

2 7 ┃10 792

A=.8(start@](],:+)pair@[)10 ┃15 330

0 1 2 3 4 5 6 7 8 ┃21 120

8 7 6 5 4 3 2 1 0 ┃28 36

┃36 8

2 3 4 5 6 7 8 9 10 ┃45 1

15 14 13 12 11 10 9 8 7

8 numerator 10

6435 10296 10296 7920 4950 2520 1008 288 45

0.3": prob_m 8 10

0.147 0.235 0.235 0.181 0.113 0.058 0.023 0.007 0.001

prob5 8 10 ┃ prob5 12 12

0.147059 ┃0.0186335 0.0774763

prob5 16 16

0.00339884 0.0186256 0.0566926

【 0.05 を１つ超えたところまでの累積確率の系列を出力する】

(p=.0.01 0.025 0.05)index 12┃ p index 16

0 1 1 ┃1 2 2

range0 12

0 6 7 8 9 10 11 12 13 14 15 16 17 18

range0 16

0 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

p percent_m 12 12 ┃ p percent_m 16 16

0 6 6 ┃8 9 9

p percent_m 20 20 ┃ p percent_m 24 24

11 12 13 ┃14 15 16

p percent_m"1(12,.12+i.5) ┃ p percent_m"1(16,.16+i.5)

0 6 6 ┃8 9 9

0 0 6 ┃8 9 9

0 0 6 ┃9 9 9

0 0 6 ┃8 9 9

　　　§６アンサリ・ブラッドレィの検定

　一般に

のような２組のデータが与えられているとする。全体を大きさの順番に並べてたものを

と置いて、

という１，０の系列に

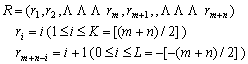
というウエィトを掛けて

という統計量を定義する。この統計量の範囲は

a = {c(c+1)+d(d+1)}/2 , c=[m/2],d=[(m+1)/2]

b = a+d×[n/2]+c×[(n+1)/2]

である。そこで、Ａという統計量がｘという値になる、ｍ個の１とｎ個の０の組合せの数をとすると、Ａの確率関数は

のように与えられる。

　Ansari-Bradley([１])は

といった漸化関係の成り立つことを示した。さらに期待値と分散も

のように与えられる。

　次のような２組のデータが与えられたとする。

　　A=:47 58 33 40 65 28 39 54 46 60 51 69

　　B=:53 44 49 56 43 55 45 57 59 52 49 48

そこで、２組のデータを大きさの順番に並べて、Ｘ(Ｙ)のデータには１(０)を付けると

U = 1 1 1 1 0 0 0 1 1 0 0 0 1 0 0 1 0 0 0 1 0 1 1 1

といった系列が得られ、これに

R = 1 2 3 4 5 6 7 8 9 10 11 12 12 11 10 9 8 7 6 5 4 3 2 1

というウエィトを掛けて加えると、統計量の値としては

A = 59

のように算出される。ところで

Pr{A(12,12)≦59} = 0.0151

という関係が得られるから、有意水準３％で等分散の帰無仮説を棄却することができる。

【Ｊ言語によるプログラム】

position=:([:/:～;)e.>@{.

weight=:[:;[:(1:+[:i.<.)L:0[:<.[:(;-)-:

stat_ab=:[:+/[:*/((weight#@;),:position

first=:((([:>.]%2:)}.(2: >:)$1:)"0

length=:1:+[:+/ .*[:[:(<.,>.)&>;

min=:[:+/]{.2:#1:+i.

range=:([:min[)+[:i.length

left=:[:+/"1[>:/([:(]%{:)+/＼)@]"1

right=:[:+/"1[>:/([:(]%{.)+/＼.)@]"1

both=:(left, .@[right])`(left,:right)@.(1:=#@[)

percent_ab=:[: :([both[:{.]){[:}.]

more=:4 :0

r=. :,.f=. .first x.+h=.0

while. h<(#{."1 y.)-1

do. b=.(a=.x.length h+1)-#s=.((>0:)#](h=.h+1){y.

r=.r,f=.((b$0),s)+f,(a-#f)$0

end.

)

table=:4 :0

r=.<q=.((k=.1)range y.),first 1+i.y.

while. k<x.

do. r=.r,<q=.(k range y.),(k=.k+1)more}.q

end.

)

position A;B

1 1 1 1 0 0 0 1 1 0 0 0 1 0 0 1 0 0 0 1 0 1 1 1

weight 24

1 2 3 4 5 6 7 8 9 10 11 12 12 11 10 9 8 7 6 5 4 3 2 1

*/ ((weight#@;),:position)A;B

1 2 3 4 0 0 0 8 9 0 0 0 12 0 0 9 0 0 0 5 0 3 2 1

+/ */ ((weight#@;),:position)A;B

stat_ab A;B

first 1+i.5 ┃ min"0(1+i.5)

2 0 0 ┃1 2 4 6 9

2 1 0 ┃ 2 length"0(1+i.5)

2 2 0 ┃2 3 4 5 6

2 2 1 ┃ 3 length"0(1+i.5)

2 2 2 ┃2 4 5 7 8

2 range"0(1+i.5) ┃ 3 range"0(1+i.5)

2 3 0 0 0 0 ┃4 5 0 0 0 0 0 0

2 3 4 0 0 0 ┃4 5 6 7 0 0 0 0

2 3 4 5 0 0 ┃4 5 6 7 8 0 0 0

2 3 4 5 6 0 ┃4 5 6 7 8 9 10 0

2 3 4 5 6 7 ┃4 5 6 7 8 9 10 11

2 more first 1+i.5

2 0 0 0 0 0 ┃f(x 2,1) , x=2,3

1 4 1 0 0 0 ┃f(x 2,2) , x=2,3,4

1 4 3 2 0 0 ┃f(x 2,3) , x=2,3,4,5

1 4 5 4 1 0 ┃f(x 2,4) , x=2,3,4,5,6,7

1 4 5 6 3 2 ┃f(x 2,5) , x=2,3,4,5,6,7,8

3 mre 2 more first 1+i.5

2 2 0 0 0 0 0 0 ┃f(x 3,1) , x=4,5

2 3 4 1 0 0 0 0 ┃f(x 3,2) , x=4,5,6,7

2 4 8 4 2 0 0 0 ┃f(x 3,3) , x=4,5,6,7,8

2 4 9 8 7 4 1 0 ┃f(x 3,4) , x=4,5,6,7,8,9,10

2 4 10 12 12 10 4 2 ┃f(x 3,5) , x=4,5,6,7,8,9,10,11

3 table 5

1 2 3

2 0 0

2 1 0

2 2 0

2 2 1

2 2 2

2 3 4 5 6 7

2 0 0 0 0 0

1 4 1 0 0 0

1 4 3 2 0 0

1 4 5 4 1 0 1 4 5 6 3 2

4 5 6 7 8 9 10 11

2 2 0 0 0 0 0 0

2 3 4 1 0 0 0 0

2 4 8 4 2 0 0 0

2 4 9 8 7 4 1 0

2 4 10 12 12 10 4 2

4 range 8

6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

]T48=.{:4 table 8

6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 4 5 4 1 0 0 0 0 0 0 0 0 0 0 0 0

1 4 7 8 9 4 2 0 0 0 0 0 0 0 0 0 0

1 4 9 12 18 12 9 4 1 0 0 0 0 0 0 0 0

1 4 9 14 22 22 21 16 9 4 2 0 0 0 0 0 0

1 4 9 16 26 32 34 32 26 16 9 4 1 0 0 0 0

1 4 9 16 28 36 44 46 46 36 29 18 11 4 2 0 0

1 4 9 16 30 40 54 60 67 60 54 40 30 16 9 4 1

+/"1}.T48

5 15 35 70 126 210 330 495

4 ! 5+i.8

5 15 35 70 126 210 330 495

]A48=.{:T48

1 4 9 16 30 40 54 60 67 60 54 40 30 16 9 4 1

0.3":100*9{.A48%495

0.202 0.808 1.818 3.232 6.061 8.081 10.909 12.121 13.535

+/＼ A48

1 5 14 30 60 100 154 214 341 395 435 465 481 490 494 495

100*8{.(]%{:)+/＼ A48

0.20202 1.0101 2.82828 6.06061 12.1212 20.202 31.1111 43.2323

100*8{.(]%{.)+/＼. A48

43.2323 31.1111 20.202 12.1212 6.06061 2.82828 1.0101 0.20202

0.005 0.025 ([>:/]%{:@]) +/＼ T

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0.005 0.025 ([:+/"1[>:/]%{:@]) +/＼ A48

1 2

0.005 0.025 left A48

1 2

0.005 0.025 right A48

16 16 15

0.005 0.025 both A48

1 2 15 16

1 2 15 16{ {.A48

7 8 21 22

('',0.005 0025 percent_m T48);T48

0 0 0 0

6 6 9 9

6 6 11 11

6 6 13 13

6 7 14 15

6 7 16 17

7 8 17 18

7 8 19 21

7 8 21 22

6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 4 5 4 1 0 0 0 0 0 0 0 0 0 0 0 0

1 4 7 8 9 4 2 0 0 0 0 0 0 0 0 0 0

1 4 9 12 18 12 9 4 1 0 0 0 0 0 0 0 0

1 4 9 14 22 22 21 16 9 4 2 0 0 0 0 0 0

1 4 9 16 26 32 34 32 26 16 9 4 1 0 0 0 0

1 4 9 16 28 36 44 46 46 36 29 18 11 4 2 0 0

1 4 9 16 30 40 54 60 67 60 54 40 30 16 9 4 1

§７２×２分割表に対するフィッシャーの精密検定

　一般に

Z =	a	b
Z =	c	d

のような２×２分割表のデータが与えられた場合、独立性の検定には「カイ２乗統計量」

を用いればよいとされている。この統計量は、ａ,ｂ,ｃ,ｄといった値がある程度大きければ、自由度１のカイ２乗分布で近似できる。ところがデータ数がかなり小さいときには、この近似が必ずしもよくないので、正確な確率の値を求めて検定を行なうべきであると、

フィッシャーが提案した。つまり、Ｚのような分割表を得る確率は、周辺度数を固定して考えるとき

という「超幾何分布」によって与えられる。例えば

B =	1	6
B =	4	2

といったデータが与えられていれば、

という確率になる。ところで与えられたデータＢと同じ周辺度数をもつ分割表は、

A		B		C		D		E		F
0	7	1	6	2	5	3	4	4	3	5	2
5	1	4	2	3	3	2	4	1	5	0	6

のように６通り考えられ、それぞれの確率は

である。分類項目の間が独立であれば、Ａという結果のほうがＢよりさらに極端なケースと考えられるから、ＡまたはＢの起きる確率は

Pr{A}+Pr{B} = 2/429 + 35/429 = 37/429 = 0.0862471

となる。５％の有意水準では、独立性の仮説を棄却できない。

【Ｊによるプログラム】

change=:(2 2$1 _1 _1 1)"_+]

translate=.4 :'change`(change^:_1)@.({.^:2=[:<./,)^:x. y.'

extreme=:([:i.1:+[:<./,)translate"0 2]

probc=:([:*/[:!+/,+/"1)%[:*/[:![:(],+/),

probe=:[:+/[:probc"_1 extreme

NB. lower 5% point

box=:[:<"_1](-,.])[:}:i.

matrix=:[:>L:1[:{L:2box@{.;[:<[: .L:0 box@{:

matrix_5=:[:((0.05"_>:L:0[:probe L:0])#L:0)matrix

eliminate=:[:(((<0 2$'')"_～:[:{."1])#])matrix

lower_5=:[:>./"_1[:>[:{."1 L:0 eliminate

index_a=:[: .(1:+4:>:])}.[:>:i.

lower_table=:<,.](];"_1[:<&lower_5"_1,.)index_a

]B=:2 2$1 6 4 2 ┃ change B

1 6 ┃2 5

4 2 ┃3 3

]A=:change^:_1 B ┃ 1 tranlate B

0 7 ┃0 7

5 1 ┃5 1

extreme B ┃ probc B

1 6 ┃0.0815851

2 4 ┃ probc 1 tranlate B

┃0.004662

0 7 ┃ prob B

5 1 ┃0.0862471

box 3 ┃ box 4

┌─-┬─-┐ ┃┌─-┬─-┬─-┐

│3 0│2 1│ ┃│4 0│3 1│2 2│

└─-┴─-┘ ┃└─-┴─-┴─-┘

matrix 4 3 　　　 ┃ matrix 4 4

┌─-┬─-┐ 　　 ┃┌─-┬─-┬─-┐

│4 0│4 0│ 　　　 ┃│4 0│4 0│4 0│

│0 3│1 2│ 　　　 ┃│0 4│1 3│2 2│

├─-┼─-┤ 　　　 ┃├─-┼─-┼─-┤

│3 1│3 1│ 　　　 ┃│3 1│3 1│3 1│

│0 3│1 2│ 　　　┃│0 4│1 3│2 2│

├─-┼─-┤ 　　　┃├─-┼─-┼─-┤

│2 2│2 0│ 　　　 ┃│2 2│2 2│2 2│

│0 3│1 2│ 　　　┃│0 4│1 3│2 2│

└─-┴─-┘ 　　　 ┃└─-┴─-┴─-┘

matrix_5 4 3 　　　 ┃ matrix_5 4 4

┌─-┬─┐ ┃┌─-┬─┬─┐

│4 0│ │ ┃│4 0│ │ │

│0 3│ │ ┃│0 4│ │ │

├─-┼─┤ ┃├-－┼─┼－┤

└─-┴─┘ ┃└─-┴─┴─┘

$ L:0 matrix_5 4 3 　　┃ $ L:0 matrix_5 4 4

┌─-┬─-┐ ┃┌─-┬─-┬─-┐

│2 2│2 0│ ┃│2 2│2 0│2 0│

├─-┼─-┤ ┃├─-┼─-┼─-┤

│2 0│2 0│ ┃│2 0│2 0│2 0│

├─-┼─-┤ ┃├─-┼─-┼─-┤

│2 0│2 0│ ┃│2 0│2 0│2 0│

└─-┴─-┘ ┃└─-┴─-┴─-┘

eliminate 4 3 　　　┃ eliminate 4 4

┌─-┬─┐ ┃┌─-┬─┬─┐

│4 0│ │ ┃│4 0│ │ │

│0 3│ │ ┃│0 4│ │ │

└─-┴─┘ ┃└─-┴─┴─┘

eliminate 5 4 　　　　┃ eliminate 5 5

┌─-┬─-┬─┐ 　┃┌─-┬─-┬─┬─┐

│5 0│5 0│ │ 　┃│5 0│5 0│ │ │

│0 4│0 3│ │ 　┃│0 5│1 4│ │ │

├─-┼─-┼─┤ 　┃├─-┼─-┼─┼─┤

│4 1│ │ │ ┃│4 1│ │ │ │

│0 4│ │ │ ┃│0 5│ │ │ │

└─-┴─-┴─┘ ┃└─-┴─-┴─┴─┘

lower_5 4 3 　　 ┃ lower_5 4

4 0 　　 ┃4 0

lower_5 5 4 　　 ┃ lower_5 5 5

5 1 　　 ┃5 1

4 0 　　 ┃4 0

(index_a 3);(index_a 4); index_a

┌-┬─-┬───-┐

│3│4 3│5 4 3 2│

└-┴─-┴───-┘

lower_table 3 　　 ┃ lower_table 4

┌-┬-┬─-┐ ┃┌-┬-┬─-┐

│3│3│3 0│ ┃│4│4│4 2│

└-┴-┴─-┘ ┃├-┼-┼─-┤

　　 ┃│4│3│4 2│

　　 ┃└-┴-┴─-┘

, lower_table 5

┌-┬-┬─-┬-┬-┬─-┬-┬-┬─-┬-┬-┬─-┐

│5│5│5 1│5│4│5 1│5│3│5 0│5│2│5 0│

│ │ │4 0│ │ │4 0│ │ │ │ │ │ │

└-┴-┴─-┴-┴-┴─-┴-┴-┴─-┴-┴-┴─-┘

, lower_table 6

┌-┬-┬─-┬-┬-┬─-┬-┬-┬─-┬-┬-┬─-┬-┬-┬─-┐

│6│6│6 2│6│5│6 1│6│4│6 1│6│3│6 0│6│2│6 0│

│ │ │5 1│ │ │5 0│ │ │5 0│ │ │5 0│ │ │ │

│ │ │4 0│ │ │4 0│ │ │ │ │ │ │ │ │ │

└-┴-┴─-┴-┴-┴─-┴-┴-┴─-┴-┴-┴─-┴-┴-┴─-┘

§８メディアン(中央値)検定

　§７では、２×２分割表に対する正確な確率の値を求めて独立性の検定を行なう方法を示した。この検定法を応用して、平均など位置母数の差異を検出する「メディアン検定」が考えられる。

　§５で考えたデータ

X=:0.1 0.2 0.2 0.4 1.3 2.4 9.3 10.8 19.9 32.5

Y=:7.6 8.4 23.5 28.7 30.3 44.7 49.1 53.2 85.2 97.3 105.1 113

に対して、全体を大きさの順に並べたときのメディアン(中央値)は、１１、１２番目のデータの平均値で「21.7」のように与えられる。この値より大きいＸのデータは１個だけで、残り９個は小さい。またＹのほうのデータについては、メディアンより小さいデータが２個で、残り１０個はメディアンより大きな値になっている。そこで

	Ｘ	Ｙ
メディアンより大きなデータ数	1	10
メディアンより小さいデータ数	9	2

といった２×２分割表が得られる。２組の標本が同一母集団からのものであれば、各マスに入るデータの個数はほぼ均等になる傾向を示すが、平均などがずれていれば、左右いずれかの対角部分に多くのデータが入るため、より偏った分割表が得られることになる。したがって、上記のような分割表の偏りの程度によって、２組の標本が同一母集団からのものであるか否かが識別できることになる。

([:(>.,<.)[:-:[:<:#)X,Y ┃ median X,Y

11 10 ┃21.7

21.7 divide X ┃ 21.7 divide Y

1 9 ┃10 2

X med_table Y ┃ probe X med_table Y

1 10 ┃0.000592608

9 2

であるから、Ｘ，Ｙに基づく分割表はかなり偏っていて、等平均の仮説は有意水準１％でも棄却できる。さらに、力士の体重に対するデータに対しても

WTW med_table WAT ┃ WTW med_test WAT

6 35 ┃6.4878e_6

37 5

W1 med_table W2 ┃ W1 med_test W2

2 8 ┃0.0115071

8 2

といった結果が得られる。１０個という少数データの場合でも、ほぼ有意水準１％で等平均の仮説が棄却できる。「メディアン検定」は、存外、検出力の高いことが分かる。

【Ｊによるプログラム】

median=:[:(+/%#)([:(>.,<.)[:-:[:<:#)

divide=:[:({:,-/)#@],[:+/<

med_table=:[: :([:median,)divide&>;

med_test=:[:probe med_table NB. median test

　　　§９各種検定法の性能(ロバストネス)の比較

　これまで紹介してきたノンパラメトリック検定法が、どの程度の識別力があるかを検討するために、乱数を使ったシミュレーション実験を行なってみよう。

　そのためにまず、分散が同じで平均だけが異なる１０個の乱数の対と、さらに平均と分散も異なるデータの対を生成する関数を次のように定義する。

unif10=.(_49.5"_+[:?10"_$100"_)%28.866"1_

NB. uniform random number

normal10=:_6:+[:+/([:?(12 10$100)"_)%100"_

NB. normal random number

dexp10=:[:-/0.7071"_*[:^.(1:+[:?(2 10$100)"_)%100"_

NB. double-exponential random number

make_data=:[:>([:<[:".[),.[:<"1(1:,{:@])*/{.@]+[:".[

NB. pair of diff. means and pair of diff. means &variences

「rand10」が一様分布、「normal10」が正規分布、そして「exp10」が両側指数分布から１０個のデータを取り出す関数で、いずれも平均が０、分散が１である。

　例えば、「unif10」に「make_data」という関数を実行してみると

'unif10 1'make_data 1 1.5

0.087 0.745 _1.299 1.230 _0.052 _0.918 0.156 0.918 _1.438 0.121

1.121 2.126 1.814 2.576 _0.230 0.706 _0.680 _0.611 0.013 2.403

0.087 0.745 _1.299 1.230 _0.052 _0.918 0.156 0.918 _1.438 0.121

1.682 3.241 2.765 3.864 _0.345 1.058 _1.020 _0.916 0.019 3.605

２つのテーブルの最初の行が平均０、分散１の分布からのデータで、最初のテーブルの最後の行が平均を１(右引数の先頭の要素)にしたときのデータで、さらにこのデータを1.5(右引数の最後の要素)倍したものが、最後のテーブルの最後の行に与えられる。

　さらに、右引数にテーブル(ランク２)を入力すると

$ U=:'unif10 1'make_data"1(10 2$1 1.5)

10 2 2 10

からも分かるように、上記のような対の２組のデータが１０セット(ランク４)生成される。　さらに、このようなＵに順位和を算出する関数を適用してみると

(82>:TEST);TEST=:({.ranksum{:)"2 U

┌─-┬───-┐

│0 1│ 85 79│

│1 1│ 70 62│

│0 0│ 83 83│

│1 1│ 74 75│

│0 0│102 102│

│1 1│ 61 63│

│1 1│ 67 66│

│1 1│ 81 71│

│1 1│ 78 75│

│1 1│ 82 68│

└─-┴───-┘

そこで、上で与えたような１０組の実験で、何回、等平均の仮説が棄却されたかは

rankt=:[:+/82>:({.ranksum{:)"2

といった関数を定義してやれば

rankt U

7 8

のようにして算出できる。さらに、連の個数による検定、メディアン検定、さらにｔ－検定等に対しても

runt=:[:+/6:>:({.nuber{:)"2

medt=:[:+/0.05"_>:({.med_test{:)"2

var_u=:[:(+/%<:@)[:*:]-mean=:+/%#

tstat=:2.236"_*[:-/[:mean&>;)%[:%:var_u

tet=:[:+/_1.734"_>:({.tstat{:)"2

のように定義して、Ｕに適用してみると

([:>rankt;runt;medt;tet)U

7 8

3 5

2 5

9 9

といった結果が得られる。

　このような実験を１０００回行なう関数を次のように定義する

simulation=:[:([:>rankt;runt;medt;tet)[make_data"1(1000 2)"_$]

]U1=:'unif10 1'simulation 1 1.5

614 720

179 281

186 303

653 792

以下同じような実験を９回行なって、結果をＵ２～Ｕ１０という変数に代入すると

U1;U2;U3;U4;U5

┌───-┬───-┬───-┬───-┬───-┐

│614 720│623 737│618 730│648 738│601 701│

│179 281│189 299│175 287│178 254│179 254│

│186 303│204 295│183 290│171 268│171 268│

│653 792│659 792│672 784│672 790│649 767│

└───-┴───-┴───-┴───-┴───-┘

U6;U7;U8;U9;U10

┌───-┬───-┬───-┬───-┬───-┐

│626 737│619 741│611 715│637 745│589 713│

│188 289│168 271│181 301│191 281│173 257│

│178 288│184 272│185 278│202 299│177 267│

│660 786│685 811│650 781│687 814│627 773│

└───-┴───-┴───-┴───-┴───-┘

のようになる。１０回分を合計して

+/U1,U2,U3,U4,U5,U6,U7,U8,U9,:U10

6186 7277

1801 2820

1863 2861

6614 7890

となる。

　さらに、正規分布や両側指数分布のデータに対しても同じ実験を行なうと

+/N1,N2,N3,N4,N5,N6,N7,N8,N9,:N10

6460 7517

1637 2546

3008 4130

6554 7672

+/E1,E2,E3,E4,E5,E6,E7,E8,E9,:E10

7657 8650

2987 4454

5273 6695

7249 8330

各結果は、上の行から順位和検定、連の個数による検定、メディアン検定、そしてｔ－検定に対するものである。総じて連の個数による検定が最も悪く、次いでメディアン検定も良くない。ところが順位和検定は、ｔ－検定と比較しても遜色ないことが分かる。特に、両側指数分布からのデータに対しては、ｔ－検定よりも良い結果になっている。

　さらに

'unif10 1'simulation 1.5 1.5

907 964

441 647

473 656

940 987

'normal10 1'simulation 1.5 1.5

930 976

449 615

647 788

939 979

'dexp10 1'simulation 1.5 1.5

956 983

604 768

815 912

953 983

のような結果が得られる。平均で１.５位離れていれば、ほぼ帰無仮説が棄却される。何故か、分散が大きく異なっている場合のほうが検出力が高い。

　なお、２組の分布が異なる場合の実験結果も示してみると

(rankt,runt,medt,tet)(unifl10,:1:+dexp10)"0 i.1000

731 256 461 692

(rankt,runt,medt,tet)(normal10,:1:+dexp10)"0 i.1000

731 259 461 723

といった結果が得られる。順位和検定がややｔ－検定を上まわるかなという感じである。

　さらに平均が１.５離れている場合の実験結果では、順位和検定やｔ－検定では、ほぼ帰無仮説が棄却される。何故か、分散が大きく異なっている場合のほうが検出力が高い。また、２組の分布が異なる場合についても実験してみると、順位和検定がややｔ－検定を上まわる感じである。

　最後に、置換検定と順位和検定の比較をしてみるために、５個のデータを生成するための関数を

unif5=:(_49.5"_+[:?(5$100"_)%28.866"1_

normal5=:_6:+[:+/([:?(12 5$100)"_)%100"_

dexp5=:[:-/0.7071"_*[:^.(1:+[:?(2 5$100)"_)%100"_

と定義し、さらに順位和検定と置換検定の実験結果を与える関数も次のように与える。

rankt55=:[:+/19"_>:({.ramksum{:)"2

C55=:comball 5 5

permt55=:[]+/12.6"_>({.([:+/"1+/@[>:+/"1 C55"_#,){:)"2

　１０００回のシミュレーションの結果は以下のようになる。

(permt55,:rankt55)'unif5 1'make_data"1(1000 2$1 1.5)

368 471

357 459

(permt55,:rankt55)'unif5 1'make_data"1(1000 2$1.5 1.5)

686 814

643 776

(permt55,:rankt55)'normal5 1'make_data"1(1000 2$1 1.5)

432 508

422 487

(permt55,:rankt55)'normal5 1'make_data"1(1000 2$1.5 1.5)

658 774

649 736

(permt55,:rankt55)'dexp5 1'make_data"1(1000 2$1 1.5)

510 611

512 601

(permt55,:rankt55)'dexp5 1'make_data"1(1000 2$1.5 1.5)

762 853

735 828

　総じて、置換検定のほうが順位和検定よりわずかながらよい。

以上の実験結果から、次のような結論が得られる。

分布が比較的かたまった状態で分離している場合にはｔ－検定が良い。

分布が正規分布より散らばっているケースでは順位和検定が良い。

また、分布形が異なる感じで分離しているときも順位和検定が良い。

データが少なく、間隔尺度なら置換検定が良いが、順位和検定でも構わない。

連の個数やメディアン検定を積極的に使う理由はなさそうである。

§１０逐次差の符号によるランダムネスの検定

　ある講座での出席者数を１回目から１０回目まで数えてみたら

講義回数	1　　2　　3　　4　　5　　6　　7　　8　　9　　10
出席者数	128　113　110　100　108　101　104　 98　 92　 82

のような結果が得られたとする。これより、出席者数は減少傾向にあるといえるだろうか？　隣あった回数の間で、出席者数が減少していれば「０」、増加していれば「１」をつけてみると、(４,５)と(６,７)のところだけが１で、残りの７か所では０である。

　一般に、

という観測系列が与えられたときに

といった統計量を定義すると、増加傾向にある個数を示す値である。

　Ｙ(ｎ)の期待値と分散は

E{Y(n)} = (n-1)/2 , V{Y(n)} = (n+1)/12

のように与えられる。さらに、を{１,２， ………, ｎ}の置換の中でY(n)＝ｋとなる組合せの数とすると、

といった漸化関係の成り立つことが分かる。ｎ個の観測系列がランダムであるという仮説の下では、確率の値が

のように与えられる。したがって

Pr{Y(n)≦y(n,α)} ≦ α

となるｙ(ｎ,α）が表１のように与えられる。

例題の場合には、Ｘ(10)＝２であるから、有意水準２.５％でランダムネスの仮説が棄却でき、出席者数は減少傾向にあると判断できる。

表1 の表

１％　2.5％　５％

0　　 0　　 0

0　　 1　　 1

1　　 1　　 1

1　　 1　　 2

1　　 2　　 2

2　　 2　　 2

2　　 3　　 3

3　　 3　　 3

3　　 3　　 4

3　　 4　　 4

【Ｊによるプログラム】

stat_line=:[:+/{:<{.

more=:[:+/([:(,.|.)1:+i.@>:@#)*[:>2:<;.0＼0:,]0:

point_line=:4 :'<:+/"1 x.>:/+/＼(more^:(y.-1)1)%!y.'

X=:128 113 110 100 108 101 104 98 92 82

(}:<}.)X

0 0 0 1 0 1 0 0 0

stat_line X

(1:+i.@>:@#)1 1 ┃ (0:,]0:)1 1

1 2 3 ┃0 1 1 0

([:(,.|.)1:+i.@>:@#)1 1 ┃ ([:>2:<;.0＼0:,]0:)1 1

1 3 ┃1 0

2 2 ┃1 1

3 1 ┃0 1

(([:(,.|.)1:+i.@>:@#)*[:>2:<;.0＼0:,]0:)1 1

1 0

2 2

0 1

more 1 1 ┃ more^:2(1 1)

1 4 1 ┃1 11 11 1

more^:3(1 1) ┃ more^:4(1 1)

1 26 66 26 1 ┃1 57 302 302 57 1

more^:5(1) ┃ +/more^:5(1)

1 57 302 302 57 1 ┃720

(i.10),:more^:9(1)

0 1 2 3 4 5 6 7 8 9

1 1013 47840 455192 1310354 1310354 455192 47840 1013 1

+/more^:9(1) ┃ !10

3628800 ┃3.6288e6

0.01 0.025 0.05 point_line 10

1 2 2

　§１１全ての対の符号によるランダムネスの検定

　観測系列のｉ＜ｊというペア(Ｘi,Ｘj)に対して、Ｘi＜Ｘjなら｢１｣、Ｘi≧Ｘjなら｢０｣を与えて、

といった統計量が定義できて、これまた増加傾向にある個数を示す値で、０から nＣ2＝

ｎ(ｎ－１)/２の範囲の値をとり、Ｚ(ｎ)の期待値と分散は

E{Z(n)} = n(n-1)/4 , V{Z(n)} = n(n-1)(2n+5)/72

のように与えられる。さらに、を{１,２，………,ｎ}の置換の中でZ(n)＝ｋとなる組合せの数とすると、

　例えばｎ＝４の場合、からまでの値が｛１,３,５,６,５,３,１｝だから

Pr{Z(4)=0}=Pr{Z(4)=6}= 1/24　，Pr{Z(4)=1}=Pr{Z(4)=5}= 3/24

Pr{Z(4)=2}=Pr{Z(4)=4}= 5/24　，Pr{Z(4)=3}= 6/24

といった具合に算出される。

　一般に

Pr{Z(n)≦p(n,α)} ≦ α

となるようなｐ(ｎ,α)が表２のように与えられる。

　さて与えられた例題の場合には、表２に示したように、１の個数が４であるから、有意水準１％でもランダムネスの仮説が棄却できる。

表２ランダムネスの検定のパーセント点

ｎ　１％　2.5％５％

ｎ　１％ 2.5％５％

5　　0　　 0　　 1

6　　1　　 1　　 2

7　　2　　 3　　 4

8　　4　　 5　　 6

9　　6　　 8　　 9

10　　9　 11　　12

11　 12　　14　　16

12　 15　　18　　20

13　 19　　22　　25

14　 24　　27　　29

15　 28　　32　　35

16　 34　　37　　41

17　 39　　43　　47

18　 45　　50　　54

19　 52　　57　　61

20　 59　　64　　69

21　 66　　72　　78

22　 74　　80　　85

23　 82　　89　　94

24　 91　　98　 104

25　100 　107　 114

26　109 　117　 124

27　119 　128　 135

28　130 　139　 146

29　140 　150　 158

30　152 　162　 170

31　164 　174　 183

32　176 　187　 196

33　188 　200　 210

34　202 　214　 224

35　215 　228　 239

36　229 　242　 254

37　244 　257　 269

38　259 　273　 285

39　274 　289　 301

40　290 　305　 318

45　376 　394　 410

50　473 　495　 513

60　702 　731　 755

【Ｊによるプログラム】

stat_pair=:[:+/([:+/{.<}.)＼.

distribution=:3 :'[:+/"1[:=[:stst_pair"1([:i.!)A.i.

next=:1:+[:-:1:+[:%:(8:*#)-7:

index=:[:>.[:-:1:+[:-:[:(*<:)next

take=:[:+/＼(index{.]

modify=:3 :'(t{.u),-/((-,])(#u)-t=.(#<.next)y.){."0 1 u=.take y.'

more_pair=:3 :'h,|.((1+-:(*<:)next y.)-#h){.h=.modify y.'

point_pair=:4 :'<:+/"1 x.>:/(+/＼more_pair^:(y.-1)1)%!y.'

var_pair=:((5:+2:*])*]*<:)%72"_

forth=:3 :'(y.*(y.-1)*_372 _997 _127 328 100&p.y.)%43200'"0

range_pair=:([:(]--:@{:)[:i.1:+[:-:]*<:)%[:%:var_pair

nden=:([:^[:-*:%2:)%[:%:[:o.2:

middle=:[:}.]*(0.002*i.500)"_

ndfs=:]*([:+/([:-:[:nden 0:,]),[:nden middle)%500"_

ndf=:ndfs+0.5"_

orgf=:nden*0 _3 0 1&p.

approximation=:ndf@[-orgf@[*(_3:+forth%[:*:var_pair)@]%24"_

point_ap=:[:<:[:+/"1[>:/[:(range_pair approximation"0])]

]Y=./:^:2 X.

9 8 7 3 6 4 5 2 1 0

]＼.Y ┃ ({.<}.)"1]＼.Y

9 8 7 3 6 4 5 2 1 0 ┃0 0 0 0 0 0 0 0 0

8 7 3 6 4 5 2 1 0 0 ┃0 0 0 0 0 0 0 0 0

7 3 6 4 5 2 1 0 0 0 ┃0 0 0 0 0 0 0 0 0

3 6 4 5 2 1 0 0 0 0 ┃1 1 1 0 0 0 0 0 0

6 4 5 2 1 0 0 0 0 0 ┃0 0 0 0 0 0 0 0 0

4 5 2 1 0 0 0 0 0 0 ┃1 0 0 0 0 0 0 0 0

5 2 1 0 0 0 0 0 0 0 ┃0 0 0 0 0 0 0 0 0

2 1 0 0 0 0 0 0 0 0 ┃0 0 0 0 0 0 0 0 0

1 0 0 0 0 0 0 0 0 0 ┃0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 ┃0 0 0 0 0 0 0 0 0

([:+/{.<}.)＼.) X ┃ stat_pair X

0 0 0 3 0 1 0 0 0 0 ┃4

(([:i.!)A.i.)3

0 1 2

0 2 1

1 0 2

1 2 0

2 0 1

2 1 0

([:stat_pair"1([:i.!)A.i.)3

3 2 2 1 1 0

([:=[:stat_pair"1([:i.!)A.i.)3

1 0 0 0 0 0

0 1 1 0 0 0

0 0 0 1 1 0

0 0 0 0 0 1

]D3=.distribution 3 ┃ ]D4=.distribution 4

1 2 2 1 ┃1 3 5 6 5 3 1

]D5=.distribution 5

1 4 5 9 15 20 22 20 15 9 4 1

6!:2'distribution 6' ┃ 6!:2'distribution 7'

1.15 ┃12.13

6!:2'distribution 8' ┃ 6!:2'distribution 9'

98.71 ┃out of memory

【直接計算するのは時間がかかりすぎる！】

next L:0 D3;D4;D5 ┃ index L:0 D3;D4;D5

┌-┬-┬-┐ ┃┌-┬-┬-┐

│4│5│6│ ┃│4│6│8│

└-┴-┴-┘ ┃└-┴-┴-┘

take L:0 D3;D4;D5

1 3 5 6

1 4 9 15 20 23

1 5 14 29 49 71 91 106

(3 :'((-,])(#u)-(#<.next)y.){."0 1 u=.take y.')D4

(3 :'((-,])(#u)-(#<.next)y.){."0 1 u=.take y.')D5

91 106

1 5

modify L:0 D3;D4;D5

1 3 5 6

1 4 9 15 20 22

1 5 14 29 49 71 90 101

D4 ; more_pair D3

1 3 5 6 5 3 1

D5 ; more_pair D4

1 4 5 9 15 20 22 20 15 9 4 1

]D6=.more_pair D5

1 5 14 29 49 71 90 101 101 90 71 49 29 14 5 1

($D6);(1+-:6*5);(+/D6);!6

720

D4 ; more_pair^:3(1)

1 3 5 6 5 3 1

D5 ; more_pair^:4(1)

1 4 5 9 15 20 22 20 15 9 4 1

0.01 0.025 0.05 point_pair 5┃ 0.01 0.025 0.05 point_pair 6

0 0 1 ┃1 1 2

0.01 0.025 0.05 point_pair 7┃ 0.01 0.025 0.05 point_pair 8

2 3 4 ┃4 5 6

0.01 0.025 0.05 point_pair 9

6 8 9

　　　§１２順位相関係数

　一般に、対で観測されたｎ個の個体の、各変量ごとの順位を（）,（)として、これらを通常の計量値のように考えて相関係数を求めてみると

のようになる。これは、「スピアマンの順位相関係数」と呼ばれているもので、２変量間に相関がない場合には

E{R(n)} = 0 , V{R(n)} = １/(n-1)

となる。さらにｎが３０くらい大きければ、近似的に正規分布に従う。

　２組のデータが全く同順位の場合には、順位の差の平方和は

であるから、R(n)＝１となり、反対に全く逆順のときには

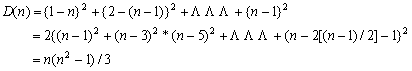
であるから、R(n)＝－１となる。

　さて、表１のデータに対する順位の差の平方和は

と算出されるから、Ｄ≦１４となる順列の総数は表２に示したように167で、また１から７までの数字の順列の総数は７！＝5040であるから

のように与えられる。したがって、無相関であるという仮説を有意水準５％で棄却でき、国語と数学の成績の間には「正の相関がある」と結論できる。

　　　順位相関係数の計算

rank=:i.@#(=/+/ .*[)/:

stst_sqd=:[:+/＼[:*:i.@#@]-rank@]/:[

stst_cor=:1:-6:*stat_sqd%[:(]**:@]-1:)#@]

seqall=:([:i.[:!#)A.] NB. all permutations

sqdall=:[:/:～[:+/"1[:*:]-"1 seqall

NB. sum of quadratic difference

sqdtable=:[:(～.,:[:+/"1=)sqdall

index=:_1:+[:+/([*[:!])>:[:+/＼]){:sqdtable@]

lower=:([*[:!])index[:sqdtable[:i.]

cvalue=:1:-6:*lower%[:(]**:@]-1:

NB. critical value of rank correlation

]RX=.rank X=:50 60 65 75 35 80 70

1 2 3 5 0 6 4

]RY=.rank Y=:40 35 80 55 25 70 45

2 1 6 4 0 5 3

*:RX-RY

1 1 9 1 0 1 0

+/*:RX-RY ┃ X stat_sqd Y

14 ┃14

X stat_cor Y

0.75

seqall i.3 ┃ sqdall i.3

0 1 2 ┃0 2 2 6 6 8

0 2 1 ┃ ]R3=.sqdtable i.3

1 0 2 ┃0 2 6 8

1 2 0 ┃1 2 2 1

2 0 1

2 1 0

sqdall i.4

0 2 2 6 6 8 2 4 6 12 10 14 6 10 8 14 16 18 12 14 14 18 18 20

]D4=.sqdtable i.4

0 2 4 6 8 10 12 14 16 18 20

1 3 1 4 2 2 2 4 1 3 1

]D5=.sqdtable i.5

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40

1 4 3 6 7 6 4 10 6 10 6 10 6 10 4 6 7 6 3 4 1

+/"1 D5

420 120

16{."1 D6=.sqdtable 6

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30

1 5 6 9 16 12 14 24 20 21 23 28 24 34 20 32

$ D6

2 36

+/"1 D6

1260 720

29{. {: D7=.sqdtable 7

1 6 10 14 29 26 35 46 55 54 74 70 84 90 78 90 123 134 147 98 168 130 175 144 168 144 168 144 184

+/"1 D7

3192 5040

43{. {: D8=.sqdtable 8

1 7 15 22 47 54 70 94 126 124 178 183 237 238 276 264 379 349 380 400 517 394 542 492 640 557 666 595 776 684 786 718 922 745 917 781 982 826 950 844 1066 845 936

$(([:i.!)A."0 1 i.) 9

out of memory

(0.05*!3)index sqdtable i.3 ┃ (0.05*!4)index sqdtable i.4

0 ┃0

(0.05*!5)index sqdtable i.5 ┃ (0.05*!6)index sqdtable i.6

2 ┃6

0.05 lower 5 ┃ 0.01 lower 5

2 ┃0

0.05 lower 6 ┃ 0.01 lower 6

6 ┃2

0.05 cvalue 5 ┃ 0.05 cvalue 6

0.9 ┃0.828571

0.05 cvalue 7 ┃ 0.01 cvalue 7

0.714286 ┃0.892857

　　　§１３順位相関係数の標本分布とパーセント点の導出

seqsum=:4 :0

'L R'=.((i.!#x.)A.x.);(i.!#y.)A.y.

r=.((k=.0){L),"1 R

while. k<<:#L

do. r=.r,((k=.k+1){L),"1 R

end.

)

sqd11=:4 :0

'L R'=.(t;-.t=.((<.-:y)=+/"1 t)#t=.#:i.-2^y=.#y.)#L:0 y.

A=.～.r [ B=.+/"1=r=./:～+/"1*:x.-"1(k{L)seqsum(k=.0){R

while. k<<:#L

do. r=./:～+/"1*:x.-"1(k{L)seqsum(k=.k+1){R

B=.+/"1((A=/～.r)#+/"1=r),.((A=./:～～.A,r)=/A)#B

end.

A,:B

)

sqd00=:4 :0

'a b'=.(d=.y.-x.)({.;}.)i.y.

'A B'=.(s;-.s=.(d=+/"1 t)#t=.#:i.-2^y.)#L:0 i.y.

C=.a sqd11 k{A [ D=.b sqd11(k=.0){B

F=.+/,.((E=./:～～.,s)=/"1 s=.({.C)+/{.D)#"_1({:C)*/{:D

while. k<<:#A

do. C=.a sqd11 k{A [ D=.b sqd11(k=.k+1){B

F=.((E=./:～～.E,t)=/E)#F [ t=./:～～.,s=.({.C)+/{.D

F=.+/"1 F,.(E=/t)#+/,.(t=/"1 s)#"_1({:C)*/{:D

end.

E,:F

)

sqd_p=:4 :'(<:+/t<{.x.){"1({.y.),:t=.+/＼({:y.)%!{:x.'

【演算時間】

6!:2'(i.k)sqd11 1;i.k=7' ┃ 6!:2'(i.k)sqd11 0;i.k=8'

0.05(0.49) ┃0.33(3.4)

6!:2'(i.k)sqd11 1;i.k=9' ┃ 6!:2'(i.k)sqd11 2;i.k=10'

2.69(33.09) ┃140.55(274.52)

6!:2'(i.k)sqd11 2;i.k=11' ┃ 6!:2'(i.k)sqd11 2;i.k=12'

1605.42(27323.5) ┃

6!:2'D9=.5 sqd00 9' ┃ 6!:2'D10=.5 sqd00 10'

2.14 ┃7.3

6!:2'D11=.6 sqd00 11' ┃ 6!:2'D12=.6 sqd00 12'

27.02 ┃102.1

6!:2'D12=.7 sqd00 12' ┃ 6!:2'D12=.8 sqd00 12'

94.96 ┃199.49

6!:2'D12=.7 sqd00 13' ┃ 6!:2'D13=.8 sqd00 13'

335.92 ┃1377.48

6!:2'D14=.7 sqd00 14' ┃ 6!:2'D15=.8 sqd00 15'

1157.5 ┃5270.49

6!:2'D16=.8 sqd00 16' ┃ 6!:2'D17=.8 sqd00 17'

18347 ┃123318

0.05 7 sqd_p D7 ┃ 0.05 8 sqd_p D8

16 0.0440476 ┃30 0.0480903

0.025 7 sqd_p D7 ┃ 0.025 8 sqd_p D8

12 0.0240079 ┃22 0.0229167

0.01 7 sqd_p D7 ┃ 0.01 8 sqd_p D8

6 0.00615079 ┃14 0.00768849

0.05 9 sqd_p D9 ┃ 0.05 10 sqd_p D10

48 0.0480903 ┃72 0.0481393

0.025 9 sqd_p D9 ┃ 0.025 10 sqd_p D10

36 0.021627 ┃58 0.0244894

0.01 9 sqd_p D9 ┃ 0.01 10 sqd_p D10

26 0.00861166 ┃42 0.00870288

0.05 11 sqd_p D11 ┃ 0.05 12 sqd_p D12

102 0.0469582 ┃142 0.0494539

0.025 11 sqd_p D11 ┃ 0.025 12 sqd_p D12

84 0.0238787 ┃118 0.0244408

0.01 11 sqd_p D11 ┃ 0.01 12 sqd_p D12

64 0.0090973 ┃92 0.0092612

0.05 13 sqd_p D13 ┃ 0.05 14 sqd_p D14

188 0.0485266 ┃244 0.0486266

0.025 13 sqd_p D13 ┃ 0.025 14 sqd_p D14

160 0.0249319 ┃210 0.0249824

0.01 13 sqd_p D13 ┃ 0.01 14 sqd_p D14

128 0.00970532 ┃170 0.00953338

0.05 15 sqd_p D15 ┃ 0.05 16 sqd_p D16

310 0.00486229 ┃388 0.0492784

0.025 15 sqd_p D15 ┃ 0.025 14 sqd_p D16

268 0.0244026 ┃338 0.0246591

0.01 15 sqd_p D15 ┃ 0.01 16 sqd_p D16

222 0.00972995 ┃284 0.00999043

0.05 17 sqd_p D17 ┃ 0.05 18 sqd_p D18

478 0.0049834 ┃580 0.0499117

0.025 17 sqd_p D17 ┃ 0.025 18 sqd_p D18

418 0.0245113 ┃512 0.0249773

0.01 17 sqd_p D17 ┃ 0.01 18 sqd_p D18

354 0.00983329 ┃436 0.00985633

【「Ｄ(n)」のパーセント点】

n 5 6 7 8 9 10 11 12 13 14 15 16 17 18

5% 2 6 16 30 48 72 102 142 188 244 310 388 478 580

2.5% 0 4 12 22 36 58 84 118 160 210 268 338 418 512

1% 0 2 6 14 26 42 64 92 128 170 222 284 354 436

　さらに高次の項を用いて連続補正を行なった場合はより改良される。

F(x) = Φ(x)-φ(x){c4H3(x)/24+c6/720H5(x)+c422H7(x)/1152

+c8H7(x)/40324+c4c6H9(x)/17280

+c43H11(x)/82944

のように表現できる。ここで

c4 = 6(36-5n-19n2)/25n(n+1)(n-1)

c6 = 48N6/245n3(n+1)3(n-1)

c8 = 144N8/875n5(n+1)5(n-1)3

N6 = -1800+2760n+4054n2-2637n3-2603n4+723n5+583n6

N8 = 846720-1080567n-1616688n2+2358048n3+1800776n4

-1690125n5-1012323n6+578442n7+304254n8-83709n9-41939n10

H3(x) = -3x+x3

H5(x) = 15x-10x3+x5

H7(x) = -105x+105x3-21x5+x7

H9(x) = 945x-1260x3+378x5-36x7+x9

H11(x) = -10395x+17325x3-6930x5+990x7-55x9+x11

である。

この近似式を用いて、パーセント点を求める関数を次のように定義する。

cum4=:_0.24"_*_36 5 19&p.%]*<:@*:

numerator6=:_1800 2760 4054 _2637 723 583&p.

cum6=:48r245"_*numerator6%*:@<:*(]*>:)^3:

numerator8=:846720 1080567 _1616688 2358048 1800776 _1690125

_1012323 578442 304254 _83709 _41939&p.

cum8=.144r875*numerator8%(<:^3:)*(]*>:)^5:

orgf3=:nden*0 _3 0 1&p.

orgf5=.nden*0 15 0 _10 0 1&p.

orgf7=.nden*0 _105 0 105 0 _21 0 1&p.

orgf9=.nden*0 945 0 _1260 0 378 0 _36 0 1&p.

orgf11=.nden*0 _10395 0 17325 0 _6930 0 990 0 _55 0 1&p.

dev1=:orgf3@[*cum4@]%24"_

dev2=:(orgf5@[*cum6@]%720"_)+orgf7@[**:@cum4@]%1152"_

dev3=:(orgf7@[*cum8@]%40324"_)+orgf9@[*(cum6*cum4)@]%17280"_) +orgf11@[*(cum4@[^3:)%82944"_

index1=:_1:+[:+/[>range0@](ndf@[-dev1+dev2+dev3)"0]

cvalue_sqd=:index1"0{range_sqd@]

0.05 0.25 0.01 cvalue_sqd 7

16 10 6

0.05 0.25 0.01 cvalue_sqd 8

30 22 14

0.05 0.25 0.01 cvalue_sqd 9

48 36 26

0.05 0.25 0.01 cvalue_sqd 10

72 58 42

0.05 0.25 0.01 cvalue_sqd 11

102 84 64

0.05 0.25 0.01 cvalue_sqd 12

142 118 92

0.05 0.25 0.01 cvalue_sqd 13

188 160 128

0.05 0.25 0.01 cvalue_sqd 14

244 208 170

0.05 0.25 0.01 cvalue_sqd 15

310 268 222

0.05 0.25 0.01 cvalue_sqd 16

388 338 282

0.05 0.25 0.01 cvalue_sqd 17

478 418 354

0.05 0.25 0.01 cvalue_sqd 18

580 512 436

PERCENTAGE POINT OF D(n) for n=4(1)30

n 5% 2.5% 1%

4 0 - -

5 2 0 0

6 6 4 2

7 16 12 6

8 30 22 14

9 48 36 26

10 72 58 42

11 102 84 64

12 142 118 92

13 188 160 128

14 244 210 170

15 310 268 222

16 388 338 284

17 478 418 354

18 580 512 436

19 694 616 530

20 824 736 636

21 970 868 756

22 1132 1018 890

23 1310 1182 1040

24 1508 1364 1206

25 1724 1566 1388

26 1958 1784 1588

27 2214 2022 1806

28 2492 2282 2044

29 2794 2564 2304

30 3118 2866 2584

【参考文献】

[1]Ansari,A.R.-Bradley,R.A.(1961).Rank-sum test for dispersions. Ann.Math.Stat.31

[1]David,S.T.,Kendall,M.G.and Stuart,A.(1951).Some questions of distribution

in the theory of rank correlation.Biometrika 38. 131-140.

[2]Kendall,M.G.,Kendall,S.F.H. and Smith,B.B.(1938).The distribution of Speaman's coefficient of rank correlation in a universe in which all rankings occur an equal number of times.Biometrika 30. 251-273.

[3]Mann,H.B.(1945).Nonparametric tests against trend.Econometrica 13. 245-259.

[2]Moses,L.E.(1952).A two sample test. Psychometrika 17

[3]Pitman,E.J.G.(1937).Significance tests which may be applied to samples from any populations. .The correlation coefficient test. J.R.S.S.Supp.4 225-232.

[４]清水良一(1976)『中心極限定理』(教育出版)