f01=: _1 1 0 1 &p.
plot _5 5 ; 'f01'
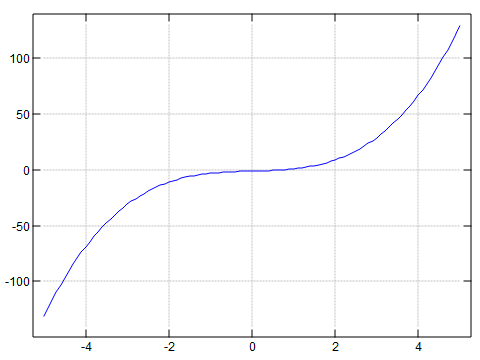
f01=: _1 1 0 1 &p.
plot _5 5 ; 'f01'

p. 35 _58 36 _10 1 +-+------------------------+ |1|4.41421 2j1 2j_1 1.58579| +-+------------------------+ 左の1は内部反復回数で苦労の目安。多いと苦労している
new_1=: 1 : ' ] - x % x D.1'(^:100) ("0)
new_11=: 1 : ' ] - x % x D.1'(^:_) ("0)
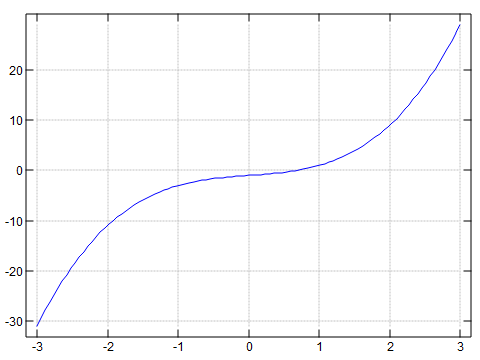
f=. _1 1 0 1&p. plot _3 3 ; 'f' |
|
_1 1 0 1&p. new_1 i:3 0.682328 0.682328 0.682328 0.682328 0.682328 0.682328 0.682328 p. _1 1 0 1 +-+---------------------------------------------+ |1|_0.341164j1.16154 _0.341164j_1.16154 0.682328| +-+---------------------------------------------+
S1=: 3 4 $ 1 2 _1 2 0 3 4 18 1 0 _1 _2 S1 1 2 _1 2 0 3 4 18 1 0 _1 _2
cr=: %. }:"1
cr S1 1 0 0 1 0 1 0 2 0 0 1 3 |
|
にJの線形計算ツールが入っている。
gauss_jordan S1 1 0 0 1 0 1 0 2 0 0 1 3
f00=: 3 : ’(ˆ{.y.)+(*/y.)-1’
g00=: 3 : ’2+(+/ y.)+1&o.*/ y.’
new_2=: 1 : ’ ] - x. (%.|:)x. D.1’ (ˆ:17) ("1)
(f0,g0) new_2 1 1 _9.41145e_6 _2